Phi Fractal Scaling
As has been observed and written about for centuries, there is a specific proportional ratio that is found throughout nature. This ratio is called Phi (often pronounced with a long "i" as in "pie" but originating from the Greek letter pronounced "fee").

Phi Basics
The Ratio
The number Phi is what's called an "irrational mathematical constant", one of those never-ending numbers like Pi. It is 1.6180339887... etc. For simplicity's sake it's commonly stated as just 1.618. This ratio has a unique property wherein when two units of different lengths are in the phi proportion, the length of the smaller unit to the larger one is of equal proportion as the length of the larger unit is to the sum of the two lengths as a whole. Here's an illustration of this property:

For the mathematically inclined, here are algebraic and mathematical formulae for phi:
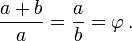 |
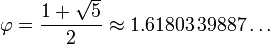
formulae source: Wikipedia
|
Fibonacci and Phi Quantities
A well-known and very simple mathematical formula that is directly related to Phi is called the Fibonacci Sequence. Quite simply, starting with 0 and 1, the sequence adds pairs of numbers to derive the next number in the sequence, like this:
0+1=1, 1+1=2, 1+2=3, 2+3=5, etc, ... deriving this sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
This sequence was first published by Leonardo of Pisa, also known as Fibonacci, in his book Liber Abaci in 1202 (though it was discovered much earlier), hence its name. It is related to phi because when you divide any pair of adjacent numbers in the sequence the result achieves an increasing accuracy to phi the farther out the sequence you go. For example (remembering phi = 1.6180339887...):
8/5=1.6
55/34=1.617647...
144/89=1.617977...
987/610=1.618032...
So, the Fibonacci Sequence is a series of numbers that have a proportionate scaling relationship approximately equal to phi. These numbers can be used as units to help illustrate proportions found in nature, and in fact can be found as actual quantities in many aspects of natural phenomena, especially in plants such as in this sunflower seed head which has 34 spirals in one direction and 55 in the other:


Comments
(please read the commenting policy before joining the conversation)