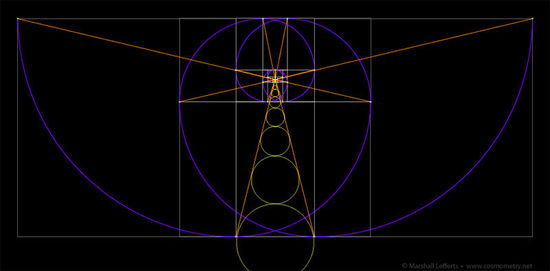
Phi Scaling Angle
Another fundamental characteristic of phi is the angle of expansion, or scaling angle, that is inherent in phi fractal scaling. This is shown in Illustration 12 where a set of circles (or spheres, the most symmetrically balanced form in nature), with diameters expanding by Fibonacci values, are placed tangential to one another in a straight line. The angle between the horizontal line at the bottom of each circle and the line that touches each circle’s “upper” surface point is the Phi Scaling Angle. This angle is approximately 27.5°. The center line angle that intersects each circle or sphere’s center point is 13.75° (which is notably 1/10th the phi rotation angle of 137.5°).

Illustration 12: Phi scaling angle, derived from circles increasing in
diameter following Fibonnaci sequence

Illustration 13: a spruce tree showing that its underlying form is a
fractal scaling based upon the phi angle

Illustration 14: a simple sea shell exhibits a close approximation to
the phi scaling angle in its growth
In this next example we can see the same angle of expansion present, yet in this case it is not a factor of growth but rather one of efficiency. Illustration 15 shows a group of pelicans soaring in a V-shaped flight pattern. As the lead bird breaks through the pressure of the air molecules it creates a vortex cone of air flow that expands behind it, a wake that reduces the impact of the wind and air for the other birds that follow. The optimum angle of relationship to experience the least drag, and therefore most efficient flight, is 27.5° (or 13.75° on either side of the lead pelican). Note, too, that these pelicans are also spaced in an expanding ratio very close to phi, as evidenced by their proximity to the tangents of the circles.

Illustration 15: pelicans in flight with phi scaling angle
Next we see that the pattern left in the sand after a wave recedes on a shoreline has a consistent "weave" based upon this same angle. This is due to the fact that the flow dynamics of water (as with all fluid dynamics, fundamentally) are phi double-spirals, stretched out upon the surface of the shore.

Illustration 16: Pattern in sand after waves receded
The same is true for the bark of certain kinds of trees that exhibit an obvious "weave" in their patterning. Again, the phi double spiral is present, this time stretched into a tubular form.

Illustration 17: Phi scaling angle found in the pattern in the bark of trees
As a final verification that this scaling angle is indeed fundamental to the phi fractal characteristics, below is an illustration of two single phi spirals, one in each rotational direction, with orange lines showing the basic differential angle between the two spirals. This angle itself is the phi scaling angle.

Comments
(please read the commenting policy before joining the conversation)